BRESENHAM'S LINE DRAWING ALGORITHM ! !

Bresenham's Line Drawing algorithm

The Bresenham algorithm is another incremental scan conversion algorithm. The big advantage of this algorithm is that, it uses only integer calculations. Moving across the x axis in unit intervals and at each step choose between two different y coordinates.

For example, as shown in the following illustration, from position (2, 3) you need to choose between (3, 3) and (3, 4). You would like the point that is closer to the original line.

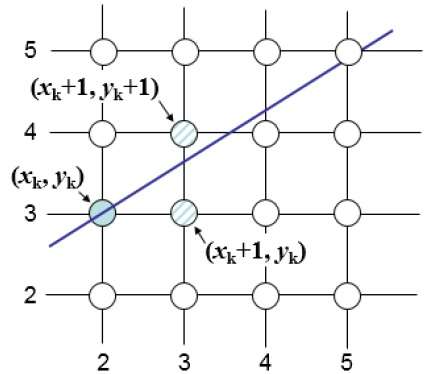
At sample position Xk+1, the vertical separations from the mathematical line are labelled as dupper and dlower.

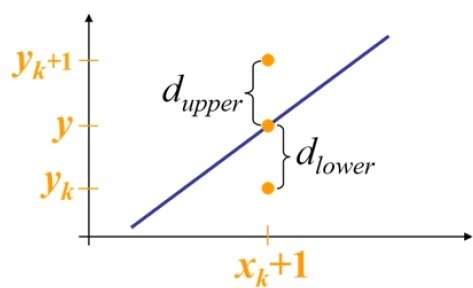
From the above illustration, the y coordinate on the mathematical line at xk+1 is −

Y = m(Xk+1) + b

So, dupper and dlower are given as follows −

dlower=y−yk

=m(Xk+1)+b−Yk

and

dupper=(yk+1)−y

=Yk+1−m(Xk+1)−b

You can use these to make a simple decision about which pixel is closer to the mathematical line. This simple decision is based on the difference between the two pixel positions.

dlower−dupper=2m(xk+1)−2yk+2b−1

Let us substitute m with dy/dx where dx and dy are the differences between the end-points.

dx(dlower−dupper)=dx(2dydx(xk+1)−2yk+2b−1)

=2dy.xk−2dx.yk+2dy+2dx(2b−1)

=2dy.xk−2dx.yk+C

So, a decision parameter Pk$P_k$ for the kth step along a line is given by −

pk=dx(dlower−dupper)

=2dy.xk−2dx.yk+C

The sign of the decision parameter Pk is the same as that of dlower−dupper.

If pk is negative, then choose the lower pixel, otherwise choose the upper pixel.

Remember, the coordinate changes occur along the x axis in unit steps, so you can do everything with integer calculations. At step k+1, the decision parameter is given as −

pk+1=2dy.xk+1−2dx.yk+1+C

Subtracting pk from this we get −

pk+1−pk=2dy(xk+1−xk)−2dx(yk+1−yk)

But, xk+1 is the same as (xk)+1. So −

pk+1=pk+2dy−2dx(yk+1−yk)

Where, Yk+1–Yk is either 0 or 1 depending on the sign of Pk.

The first decision parameter p0 is evaluated at (x0,y0) is given as −

p0=2dy−dx

Now, keeping in mind all the above points and calculations, here is the Bresenham algorithm for slope m < 1 −

Step 1 − Input the two end-points of line, storing the left end-point in (x0,y0).

Step 2 − Plot the point (x0,y0).

Step 3 − Calculate the constants dx, dy, 2dy, and (2dy – 2dx) and get the first value for the decision parameter as −

p0=2dy−dx

Step 4 − At each Xk along the line, starting at k = 0, perform the following test −

If pk < 0, the next point to plot is (xk+1,yk) and

pk+1=pk+2dy

Otherwise,

(xk,yk+1)

pk+1=pk+2dy−2dx

Step 5 − Repeat step 4 (dx – 1) times.

For m > 1, find out whether you need to increment x while incrementing y each time.

After solving, the equation for decision parameter Pk will be very similar, just the x and y in the equation gets interchanged.

// C program for Bresenham's line drawing algorithm

#include<stdio.h>

#include<conio.h>

#include<math.h>

#include<graphics.h>

#define sign(x) ((x>0)?1:((x<0)?-1:0))

// Driver program

int main()

{

      int driver,mode;

      int dx, dy, x,y, d, s1, s2, swap=0, temp,i;

      int x1,y1,x2,y2;

      driver = DETECT;

      detectgraph(&driver,&mode);

// Initialize graphics function

      initgraph(&driver,&mode,"");

      line((getmaxx()/2),0,(getmaxx()/2),getmaxy());

      line(0,(getmaxy()/2),getmaxx(),(getmaxy()/2));

      printf("Enter the two endpoints of the line:");

      printf("\nx1=");

      scanf("%d",&x1);

      printf("y1=");

      scanf("%d",&y1);

      printf("x2=");

      scanf("%d",&x2);

     printf("y2=");

      scanf("%d",&y2);

    // calculate dx & dy
dx = abs(x2 -x1);

      dy = abs(y2 -y1);

      s1 =sign(x2-x1);

      s2 =sign(y2-y1);

      if(dy > dx)

      {

            temp =dx;

            dx = dy;

            dy =temp;

            swap =1;

      }

      d = 2 * dy -dx;

      x = x1;

      y = y1;

      for(i = 1; i<= dx; i++)

      { // Put pixel for each step

            putpixel(x+(getmaxx()/2),(getmaxy()/2)-y,WHITE);

            while(d>= 0)

            {

                  if(swap)

                   x= x + s1;

                  else

                  {

             y= y + s2;

           d= d - 2* dx;

                  }

            }

            if(swap)

             y= y + s2;

            else

              x= x + s1;

            d = d +2 * dy;

      }

      getch();

      closegraph();

      return 0;

}

OUTPUT:-

Want a code for Dotted and Thick Line using Bresenham. Leave your email id in the comment box.